
|
COMPACTONS |
|
Self-similar Radiation from Numerical Rosenau-Hyman Compactons |


|
Zoom in of the snapshots of the radiation generated at both sides of a compacton propagating with c=1 at two instants of time, t=100 (top plot) and t=250 (bottom plot). The compacton was stopped using a Galilean transformation. |
|
Self-similar Radiation from Numerical Rosenau-Hyman Compactons |
|
The numerical simulation of compactons, solitary waves with compact support, is characterized by the presence of spurious phenomena, as numerically-induced radiation, wich is illustrated here using four numerical methods applied to the Rosenau-Hyman K(p,p) equation. Both forward and backward radiations are emitted from the compacton presenting a self-similar shape which has been illustrated graphically by the proper scaling. The front velocity of both radiations depends linearly on the compacton velocity. The amplitude, in both cases, decreases exponentially in time, being characterized by a nearly constant scaling exponent as a function of both the mesh grid size and the compacton velocity.
An ansatz for both the backward and forward radiations corresponding to self-similar functions characterized by scaling exponents are suggested by the present numerical results.
This web is a complement for the paper “Self-similar Radiation from Numerical Rosenau-Hyman Compactons”, that is Ander review for Journal of Computacional Physic. In this web, the generality of the numerically-induced radiation emitted by compactons is illustrated by means of extensive numerical studies using four numerical methods. |
|
Numerical Methods
Both finite element and finite difference methods without high-frequency filtering have also been proposed. In finite element methods both a Petrov-Galerkin method using the product approximation developed by Sanz-Serna and Christie~\cite{deFrutosSanzSerna1995}, and a standard method based on piecewise polynomials discontinuous at the element interfaces~\cite{LevyShuYan2004} have been used. Second-order finite difference methods~\cite{IsmailTaha1998}, high-order Pad\'e methods~\cite{RusVillatoro2005}, and the method of lines with adaptive mesh refinement~\cite{SaucezEtAl2004} has also been applied with success. These methods also require artificial dissipation to simulate the generation of shocks after compacton interactions, which is usually incorporated by a linear fourth-order derivative term.
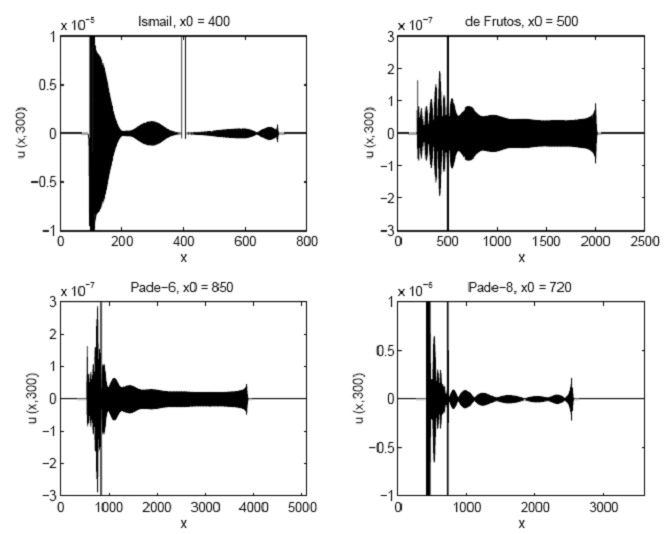
In the next figure we can see a zoom in of snapshots at t=300 of the radiation generated at both sides of a compacton propagating with c=1 numerically calculated using Δx=0.05 and Δt=0.1 by means of Ismail (top left plot), de Frutos (top right plot), Padé 6 (bottom left plot), and Padé 8 (bottom right plot) methods, initially located at, respectively, x0 =400, 500, 850, and 720. |
|
Invariants
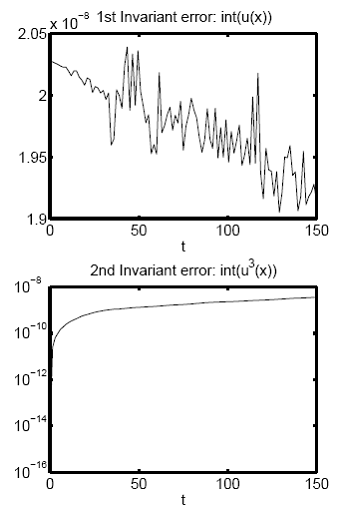
The error between the analytical value and the numerical one calculated by the trapezoidal quadrature rule for the first (top plot) and second (bottom plot) invariants during the propagation of the 1-compacton solution of the K(2,2) equation.
|

|
Next pages present our results on the properties characterizing both the forward and the backward numerically-induced radiation wavepackets generated during the propagation of one-compacton solutions.
Also, you can qualitatively appreciate those characteristics for the K(2,2) equation watching the animation files we are posted in the following table: |
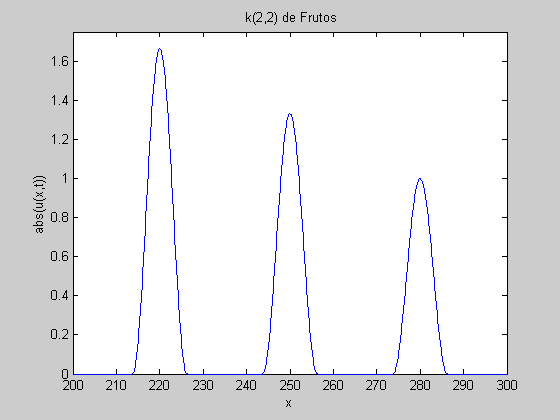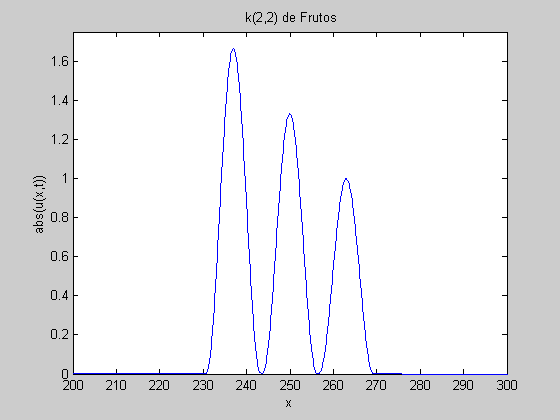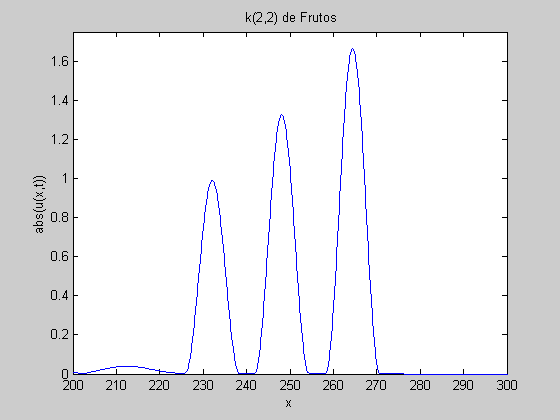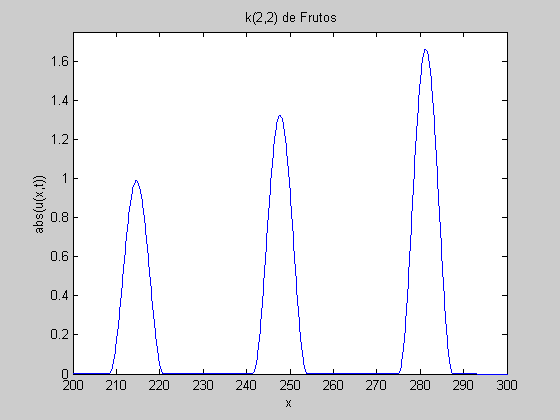
|
METHOD |
Δx |
Δx |
C |
T |
LINK |
|
Ismail |
0.05 |
0.05 |
1 |
300 |
|
|
De Frutos |
0.05 |
0.05 |
1 |
300 |
|
|
Padé 6 |
0.05 |
0.05 |
1 |
300 |
|
|
Padé 8 |
0.05 |
0.05 |
1 |
300 |